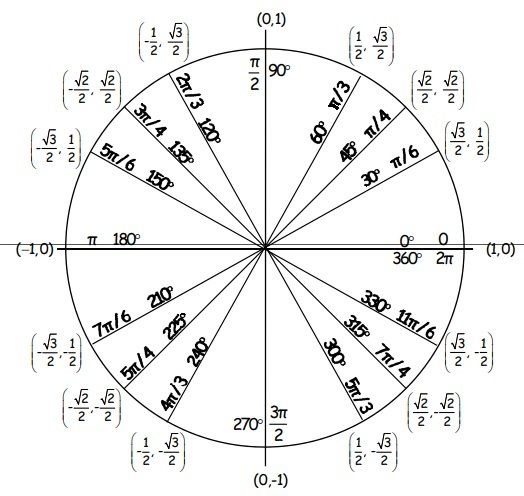
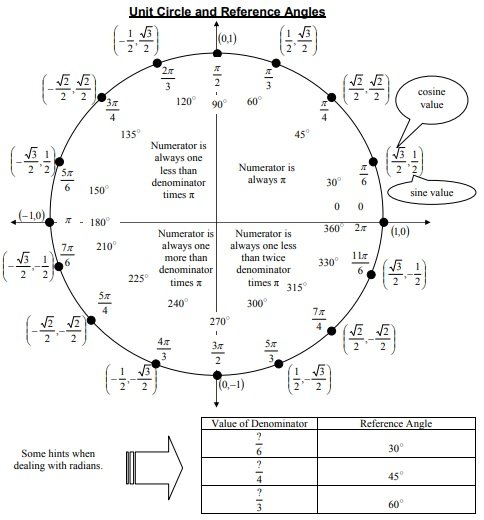
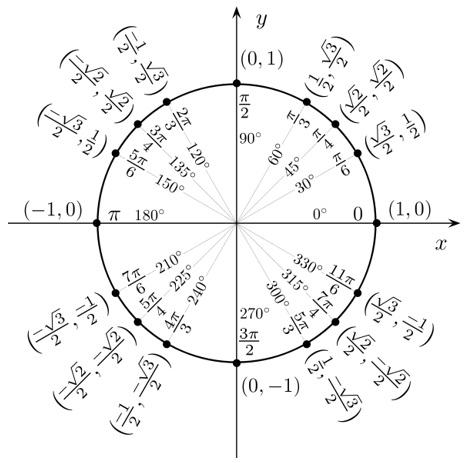
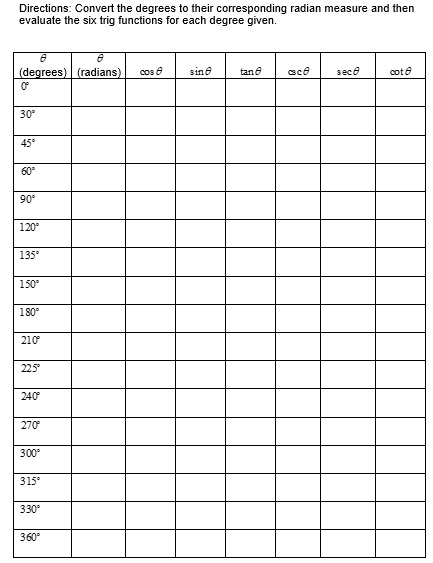
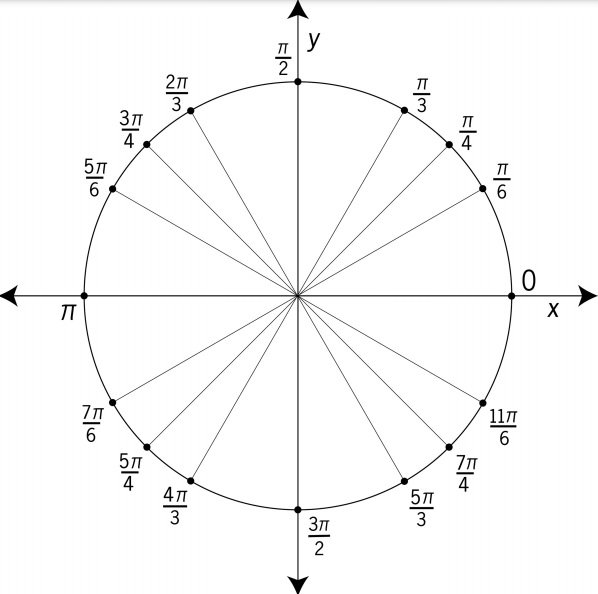
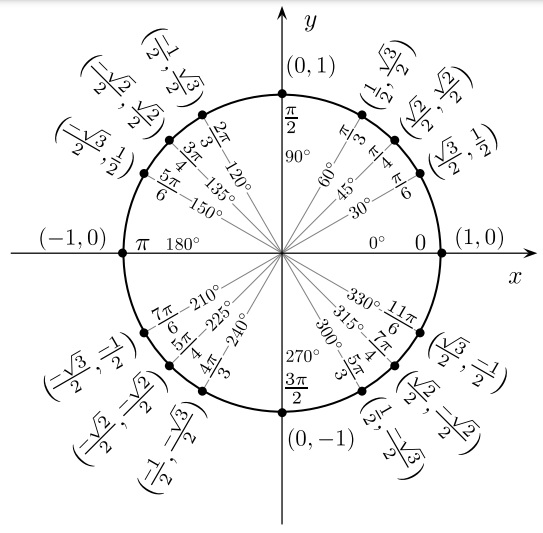
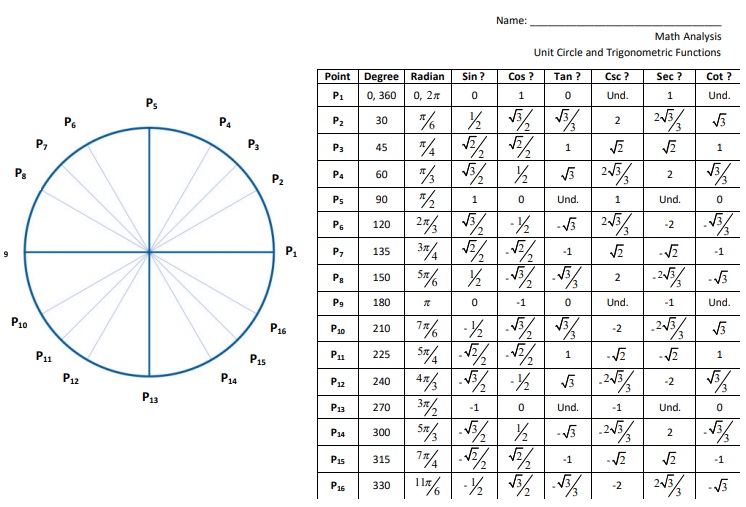
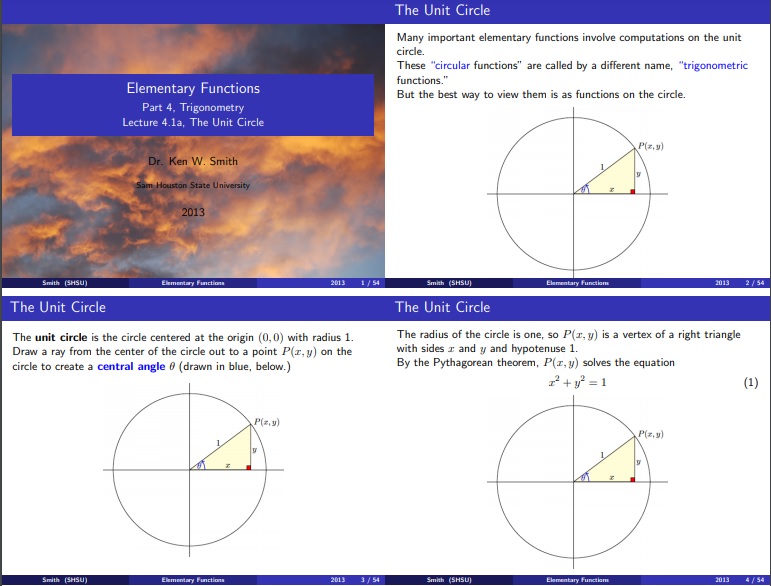
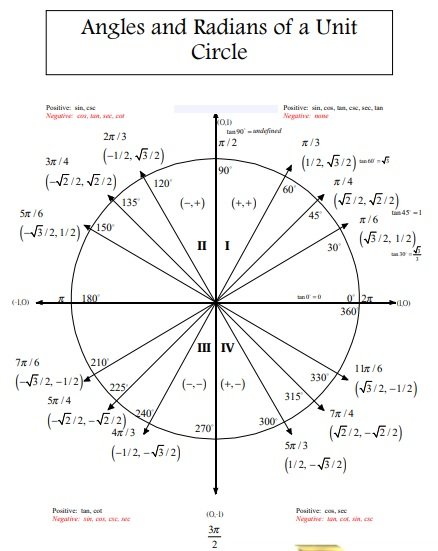
The unit circle chart represents the points and unit circle when we divide the circle into 8 or 12 parts. It is known as a unit circle because it has a one-unit radius.
Table of Contents
What basically a unit circle chart is?
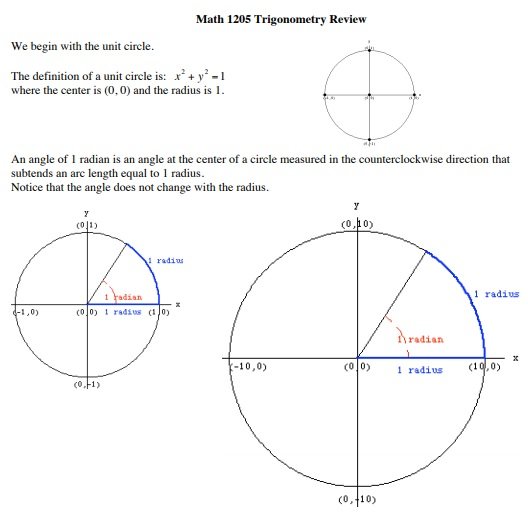
A unit circle is used in the Mathematics branch of trigonometry. This circle has different values as compared to other circles and curved shapes. You can use it to describe all possible measures of angles from 0° to 360°. It explains all the positive and negative angles in the circle. In other words, it represents all the possible angles that exist in the circle. Moreover, it gives a wide range for measuring angles. Therefore, people use it rather than the right triangle.
The main purpose of the unit circle chart is to find the trigonometric ratios and functions. For instance, you can use the value of cosine and sine at any angle in the unit circle. You can use unique values such as y= sin (θ) or x= cos (θ). At the center of a circle, some angles have the same trigonometric values. The half-unit circle is equal to 2pi or 2π. You may also like the Chore Chart Template.
How to create your own unit circle chart?
Here are some steps that you can use to make your unit circle chart;
Step#1:
At first, start by making the first quadrant on a unit chart. Now, plot 30° for your unit circle.
Step#2:
Take a point and join it to the origin by drawing a straight line. Also, ensures that the terminal side of the angle is in the first quadrant and angle size is small.
Step#3:
Next, sketch a perpendicular line. Now, you can easily create a right triangle. The hypotenuse of the right triangle is basically the radius of your unit circle. One side of the triangle is on the x-axis i.e. base and one side is on the y-axis i.e. perpendicular.
Step#4:
The next step is to measure the length of the hypotenuse. As we know that the hypotenuse represents the radius of a circle and the radius of the circle is 1 so the length of hypotenuse would also be 1.
Step#5:
After that, find the lengths of the other two sides. To find them, select the shorter side. To find the length divide the value by two. On the other hand, you can find the length of the long side by multiplying the value of the short side by 2.
Step#6:
Next, you have to determine the point in your circle. A unit circle has the origin at its center. So, every point has different coordinates. By now, you can easily assign a name to the point at the 30° on your circle.
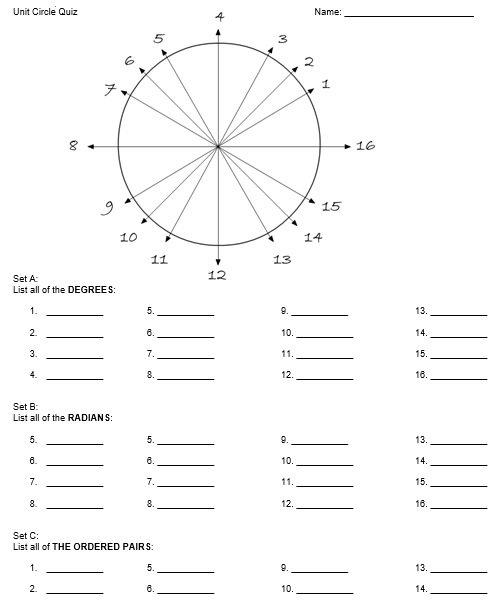
When you have all done with the above steps, it becomes easy for you to find the points of different angles on your circle. However, the second and fourth quadrants are the reflected images of the first quadrant. But their signs are different because they are placed at different locations of the plane. You should also check the Multiple Choice Test Template.
Some facts about a trigonometric circle chart:
There are some facts that you should know about a trigonometric circle chart;
- In the 1st quadrant, both x and y have positive values.
- In the 2nd quadrant, x has a negative value and y has a positive.
- In the 3rd quadrant, both x and y have negative values.
- In the 4th quadrant, x has a positive value and y has a negative.
How to understand the unit circle chart?
When you are studying trigonometry you can use a unit circle chart. This is the best tool to use. You can either download a unit circle printable or create your own. Here are some guidelines that will help you in understanding the unit circle chart;
- At first, you should know what a unit circle chart is. As we discussed above that it’s a circle having a radius of 1 and centered at the origin. Furthermore, this tool will help you to find trigonometric ratios and functions.
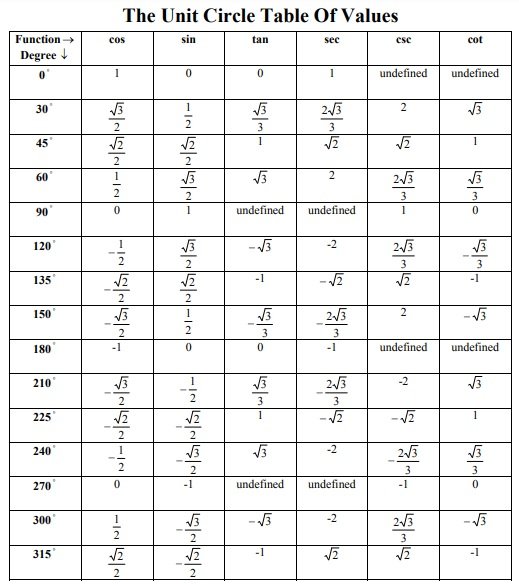
- A unit circle has 6 trigonometric ratios that you must know to understand the chart;(i). sinθ= perpendicular/hypotenuse
(ii). cosθ= base/hypotenuse
(iii). tanθ= perpendicular/base
(iv). cosecθ= 1/sinθ
(v). secθ= 1/cosθ
(vi). cotθ= 1/tanθ - After this, you should also know what a radian is. Basically, a radian is a way or unit to measure different angles. You should also know how many radians are there in the entire circle. A complete circle has 2π radians. In addition, know how to convert between degrees and radians. Let us discuss below some quick conversions;
• 2π radians= 360°
• 1 radian= 360°/2π or 1°= 2π/360
• 1 radian= 180/ π or 1°= π/180 - You should also know about some special angles such as π/6, π/3, π/4, π/2, π, and their multiples.
- The trigonometry identities which gives 6 basic functions for angles are;
• Sinθ= y
• Cosθ= x
• Tanθ= y/x
• Cosecθ= 1/y
• Secθ= 1/x
• Cotθ= x/y - Most importantly, you should know the values of the 6 basic trigonometric functions of π/6, π/3, and π/4. All these are special reference angles. You may also see Graph Paper Template.
What are the different advantages of the unit circle chart?
Using a unit circle chart will provide you various advantages that are discussed below;
- The main benefit of the unit circle chart is that it enables you to solve trigonometric functions of any radian or degree. You need this chart in mathematics, physics, and applied sciences like chemistry and geography. Hence, you have to understand it to pass several subjects.
- Most importantly, it helps the students to memorize the various concepts of mathematics easily. Sometimes, students have to memorize over 15 angles but with the help of the unit circle chart, there is no need to memorize them.
- Just like different subjects, trigonometry is a broad branch of mathematics. It is used in several fields such as construction, aerodynamics, shooting, engineering, etc.
Hence, we conclude that a unit circle chart helps you to understand mathematics and trigonometry easily. It also helps its users to learn about the circle angles. However, it is an essential tool for student’s success.
Faqs (Frequently Asked Questions)
The form (cos (θ), sin (θ)) are the coordinates of the points on the unit circle. Here, θ is the angle that measures in radians.
The special angles in the unit circle are as follows;
1- 0
2- π/2
3- π
4- 3π/2
5- 2π
On the unit circle, these special angles correspond to the points (1, 0), (0, 1), (-1, 0), (0,-1), and (1, 0).
The radian is the unit of measurement for angles in the circle.
The unit circle is used in mathematics, physics, and engineering. It is used to find the lengths of the arc, sector, and segment in the circle. Trigonometric functions of complex numbers can also be defined by using the unit circle.